BAB 3 RELASI DAN FUNGSI (Subbab Relasi) kelas VIII Semester 1

SILAHKAN TEMAN-TEMAN BISA BELAJAR MELALUI CHANNEL YOUTUBE YANG DISEDIAKAN 

MATEMATIKA KELAS VIII BAB 2 (KOORDINAT KARTSIUS)

 

BARISAN ARITMATIKA

RUBRIK PENILAIAN KUIS POLA BILANGAN KELAS VIII

RUBRIK PENILALIAN PENGETAHUAN

Mata Pelajaran            : Matematika

Kelas/ Semester           : VIII/1

Kompetensi Dasar       : 3.1 Pola Bilangan

Bentuk Soal                : Pilihan Ganda

NO.	Indikator Soal	Soal	Ranah Kognitif	Kunci Jawaban	Skor
1.	Mengetahui macam-macam pola barisan bilangan.	berikut adalah macam-macam pola barisan bilangan, kecuali .... a.    pola bilangan bulat (bilangan ganjil dan bilangan genap) b.   pola persegi dan persegi panjang c.   pola segitiga dan pola segitiga pascal d.  pola belah ketupat dan pola jajargenjang	C2	D	10
2.	Mengamati pola pada suatu barisan bilangan	Perhatikan pola bilangan (3,6), (6,15), (8,21). pernyataan yang tepat untuk mendapatkan bilangan kedua dari pasangan bilangan pertama pada pola tersebut adalah .... a.   ditambah 3 b.   dikalikan 2 c.   dikalikan 3 kemudian dikurangi 3 d.  dikalikan 2 kemudian ditambah 3	C4	C	10
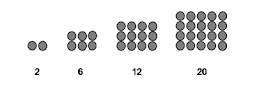
3.	Menemukan pola ke-n pada pola barisan persegi panjang.	Banyak kelereng pada pola berikutnya adalah .... a.   25 buah b.   30 buah c.   35 buah d.  40 buah	C4	B	10
4.	Menggeneralisasi pola barisan bilangan menjadi suatu persamaan	Rumus suku ke-n dari barisan di bawah adalah.... a.       nxn b.      n(n+1) c.       1/2 x n x (n+1) d.      n(n-1)	C5	C	10
5.	Menemukan pola ke-n pada pola barisan segitiga pascal	jumlah baris ke-5 pada pola segitiga pascal di bawah adalah .... a.       8 b.      16 c.       32 d.      64	C4	B	10
6.	Menggeneralisasi pola barisan bilangan menjadi suatu persamaan	Dalam pola bilangan segitiga pascal, rumus untuk menentukan jumlah bilangan pada baris ke-n adalah....	C5	B	10
7.	Menggeneralisasi pola barisan bilangan menjadi suatu persamaan	Rumus ke-n dari barisan 3, 6, 11, ... adalah ....	C5	A	10
8.	Mengamati pola pada suatu barisan bilangan	10, 30, 50, 70, ...., .... a.       80,90,100 b.      90,110,130 c.       100,200,400 d.      110,130,150	C3	B	10
9.	Menentukan suku selanjutnya dari suatu barisan bilangan dengan cara menggeneralisasi pola bilangan sebelumnya.	perhatikan pola barisan persegi berikut. 1, 4, 9, 16, ....,.... . suku ke-25 adalah .... a.       100 b.      225 c.       625 d.      1024	C5	C	10
10.	Menentukan suku selanjutnya dari suatu barisan bilangan dengan cara menggeneralisasi pola bilangan sebelumnya.	batang korek api disusun dengan susunan seperti gambar di bawah. jika pola tersebut terus berlanjut, banyak batang korek api pada susunan ke-10 adalah .... a.       33 b.      36 c.       39 d.      42	C5	A	10

 

Total skor = 100

                                                                                                            Semarang, 3 Agustus 2020

Kepala SMP N 43 Semarang                                                              Guru Mata Pelajaran

 

 

 

Ripto, S.Pd., M.Pd                                                                            Hafidlotul Rif’ah, S.Pd.

NIP. 19691231 199802 1 003                                                             NIP. -